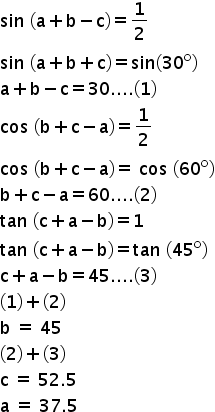Sin A B 1 2 Cos A B 1 2 Find Angle A
If Sin A B 1 2 Cos A B 1 2 Then Find The Value Of A Amp B Brainly In
.gif)
If Sin A B 1 2 And Cos A B 1 2 Then Find Angle A Mathematics Topperlearning Com I2mift00
Sir If Sin A B 1 2 Cos A B 1 2 Find A B Mathematics Topperlearning Com N2bp87cc
Example 8 If Sin A B 1 2 Cos A B 1 2 Find A
Example 8 If Sin A B 1 2 Cos A B 1 2 Find A
If Cos A B 0 And Sin A B 1 2 Then Find The Value Of Aand B Where Aand B Are Acute Angle Brainly In
Learn more trigonometry formulas at byju s.
Sin a b 1 2 cos a b 1 2 find angle a. It s used to expand sin of subtraction of two angles functions such as sin a b sin x y sin alpha beta and so on. Sin θ tan θ and 1 are the heights to the line starting from the x axis while cos θ 1 and cot θ are lengths along the x axis starting from the origin. You can find basic trigonometry formulas identities triple angle and double angle formulas. This angle a b is likely going to be in quadrant 4 since the value of sine for a is in the negative while both cosine values are positive for both a and b.
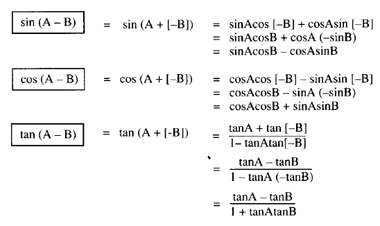
You know how to expand sin of difference of two angles and it s essential to learn how it is derived in mathematical form in trigonometry. Sin and cos formulas are given in this article. 10 class trigonometry most important question. The main idea is to create a triangle whose angle is a difference of two other angles whose adjacent sides out of simplicity are both 1.
The points labelled 1 sec θ csc θ represent the length of the line segment from the origin to that point. Given data our equations are a b 30 1 a b 60 2 adding 1 and 2 a b a b 60 30 2a 90 a 90 2 a 45 putting a 45 in 2 a b 60 45 b 60 b 60 45 b 15 hence a 45 b 15. Plot of the six trigonometric functions the unit circle and a line for the angle θ 0 7 radians. Note that the three identities above all involve squaring and the number 1 you can see the pythagorean thereom relationship clearly if you consider the unit circle where the angle is t the opposite side is sin t y the adjacent side is cos t x and the hypotenuse is 1.
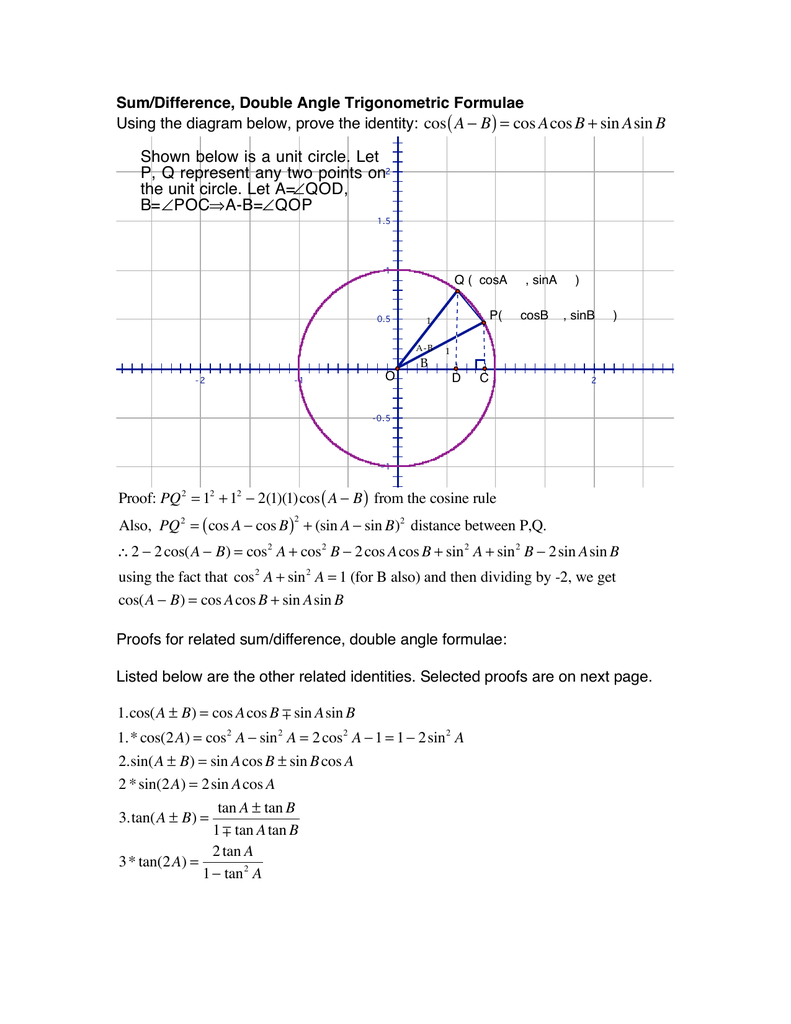
I missed the negative sign for sqrt 3 2 earlier so i might have given you an erroneous answer. By using both the distance formula and the law of cosines we can get an equation where cos a b is present. A proof that cos a b cosacosb sinasinb. 2 sin a b sin a b in the proofs the student will see that the identities e through h are inversions of a through d respectively which are proved first.
We have additional identities related to the functional status of the trig ratios.
If Cos A B 1 2 And Sin A B 1 2 Then Find The Smallest Value Of A And B Youtube
If Sin A B 1 And Cos A B 3 2 Find The Value Of A Andb Brainly In
If Sin A B 1 And Cos A B 1 Find A And B Experts Please Explain The Solution Step By Step Brainly In
In The Acute Angle Triangle Abc If Math Sin A B C Frac 1 2 Text And Cos B C A Frac 1 Sqrt 2 Math How Do I Find Angle A Angle B And Angle C Quora
In An Acute Angled Triangle Abc If Sin A B C 1 2 And Cos B C A 1 2 Find A B And C Sarthaks Econnect Largest Online Education Community
In The Acute Angle Triangle Abc If Math Sin A B C Frac 1 2 Text And Cos B C A Frac 1 Sqrt 2 Math How Do I Find Angle A Angle B And Angle C Quora
If Cos A B 1 2 And Sin A B 1 2 Find The Smallest Positive Values Of A And B Youtube
Pinkmonkey Com Trigonometry Study Guide 4 5 Factorization And Defactorization
New Page 1
Answered 19 Cos X Cos 2x 0 20 Sin X Cos 2x Bartleby
If Sin A B 1 And Cos A B 1 Find The Value Of A And B Brainly In
Half Angle Identities
New Page 1
Trigonometric Ratios And Identities 1
Sin 45 A Sin 45 A 1 2 Cos A Sin A Prove Trigonometric Ratios Of Compound Angles Trigonometry Sci Pi Sci Pi Science And Mathematics Notes With Solutions
No 1 If Each Of A B Andc Is A Positive Acute Angle Such That Sin A B C 1 2 Cos B C A 1 2 And Tan C A B
If A B And C Are Angles Of A Triangle Then Show That Sin A B 2 Cos C 2 Quora
A 2 Cos2b B 2 Cos 2a 2 Ab Cos A B C 2 Youtube
Sin A Sin B
Prosthaphaeresis Wikipedia
New Page 1
Cos Acosb Sin Asinb
Find Measure Of The Angles A And B If Cos A B Root3 2 And Sin A B Root3 2 Brainly In
Solution Of Triangles
Solved Question 5 Calculate Acute Angles Only Without Chegg Com
Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
How Do You Evaluate Cos 1 1 2 Socratic
Solved Trig Identities In Class I Wrote The Following Tri Chegg Com
Trigonometry Cl 10 Notes
A To Use The Formulae Sin A B Cos A B And Tan A B B To Derive And Use The Double Angle Formulae C To Derive And Use The Half Angle
Pinkmonkey Com Trigonometry Study Guide 4 5 Factorization And Defactorization
Rd Sharma Solutions For Class 10 Chapter 5 Trigonometric Ratios Exercise 5 1 Get Pdf For Free
Ex 8 3 6 Show That Sin B C 2 Cos A 2 Chapter 8 Class 10
